
Sabrina Grillo, Université Paris-Est Créteil Val de Marne (UPEC)
Le nombre d’or, nommé aussi proportion divine, dicte un rapport harmonieux entre les différentes parties d’un objet ou d’une image. Le mathématicien Étienne Ghis, dans un article du Monde rappelle ainsi que :
« Lorsqu’on décompose un objet en deux parties inégales, on dit que la proportion est divine, ou dorée, si le rapport entre la grande partie et la petite est le même que le rapport entre le tout et la grande partie. »
On le représente par le nombre φ phi (fi) et a un lien direct avec le nom du sculpteur grec Phidias à l’origine de la façade du Parthénon d’Athènes. Sa valeur est de 1,61803398874989482045… résultat d’une équation mathématique connue depuis la Grèce antique, à savoir (1+√5)/2.
C’est bien le langage mathématique qui est à l’origine de notions esthétiques telles que la proportion, l’harmonie ou le principe de symétrie. Selon le mathématicien Hermann Weyl : « tous les résultats a priori de la physique ont leur origine dans la symétrie ».
Beauté et bonté
Dès l’Antiquité donc, les vertus esthétiques prêtées au nombre d’or sont multiples et tendent à dépasser rapidement l’harmonie et l’équilibre de l’organisation spatiale. Elles sont ainsi largement transposées à l’équilibre intérieur de l’être et des âmes. Aussi, pour Aristote, le beau est nécessairement harmonieux et proportionné ; pour Socrate et Platon, un corps beau ne peut être que le reflet d’une âme belle. Cette équation helléniste garde une empreinte très forte dans notre civilisation : souvenez-vous des contes de fées dans lesquels tous les princes et princesses sont beaux et belles ; les bons sont beaux et les méchants beaucoup moins.
Le mathématicien italien Leonardo Pisano, dit Fibonacci, né en 1175, est parvenu à élaborer une suite, que l’on appelle communément la suite de Fibonacci. Elle repose sur le fait de diviser un terme par le précédent, chaque nouveau résultat s’approchant de plus en plus… du nombre d’or. Tom Hanks, dans Da Vinci Code, tente de décoder un message sur une scène de crime : ce n’est autre que cette suite de Fibonacci. L’architecture de la pyramide du Louvre, inspirée des pyramides égyptiennes, repose sur des proportions proches de celles définies par le nombre d’or. Même le triangle d’or parisien s’inscrit dans le rapport du nombre d’or.
Définir le beau
À travers les mathématiques, les arts, les sciences ou la philosophie, toutes les civilisations ont tenté de définir le beau. Dans l’antiquité, divers théoriciens de la sculpture ont préétabli des canons de beauté à partir de cette idée de justes proportions, d’un tout harmonieux. Le canon dit de Polyclète défendait ainsi qu’un corps beau devait être égal à sept fois la hauteur de la tête. Jusqu’à la Renaissance, le beau n’est que mimesis de la nature organisée et structurée par l’équilibre du nombre d’or. Cette proportion « divine » aidait à reproduire la divine création en copiant son équilibre. Dès lors, les canons de beauté traduisent une nouvelle vision de l’homme, plus anthropomorphe.
Léonard de Vinci a appliqué la divine proportion à l’Homme de Vitruve, une sorte d’homme idéal, donnant forme à la théorie selon laquelle la nature et donc le corps de l’homme est l’exemple même de l’équilibre des proportions. Le nombril étant le point central du corps humain ainsi que du carré dans lequel il est intégré. Cette application du nombre d’or en Grèce et à Rome jusqu’à la Renaissance traduit une idéalisation du beau – dont se font l’écho Léonard de Vinci, Boticcelli ou encore Michel-Ange.
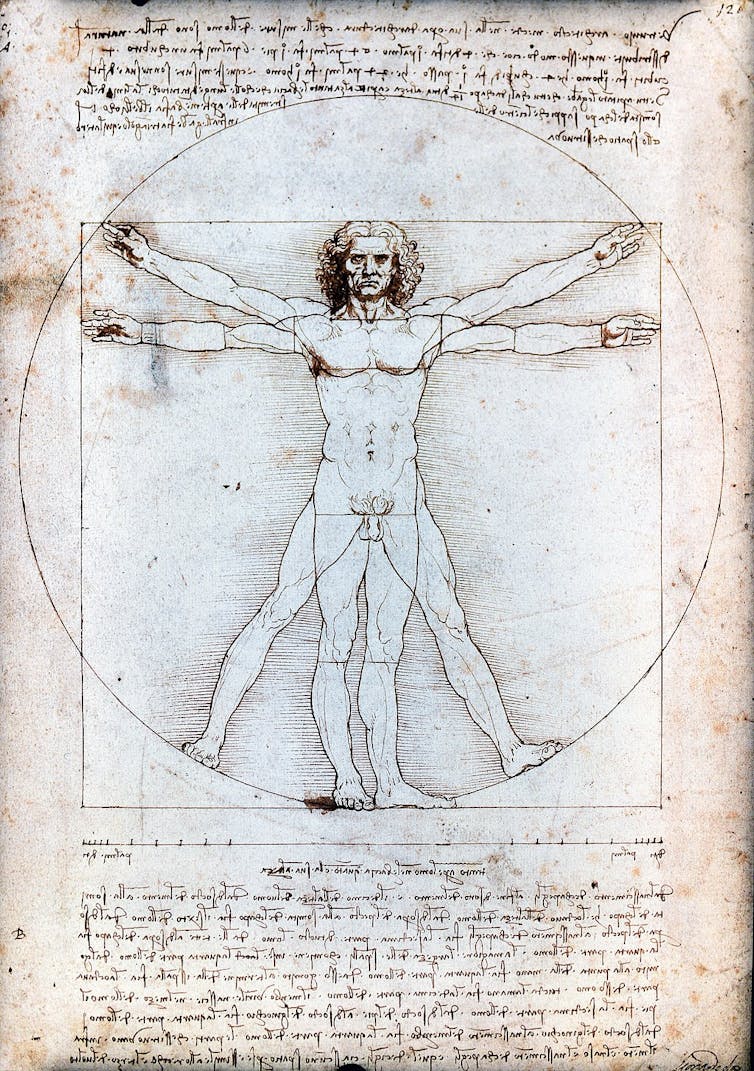
Vitruve, architecte romain qui vécut au Ier siècle av. J.-C., estimait en effet que :
« Pour qu’un bâtiment soit beau, il doit posséder une symétrie et des proportions parfaites comme celles qu’on trouve dans la nature. »
Nombre d’artistes se sont inspirés des multiples modèles géométriques offerts par la nature pour parvenir à des œuvres aux proportions harmonieuses et c’est toujours le cas à l’époque contemporaine. Au milieu du XXe siècle, art, architecture, nature et mathématiques se croisent encore dans le système de mesure du Corbusier : le Modulor.
La nature a été aussi la plus grande source d’inspiration de l’architecte catalan Gaudí. Pensez aux colonnes semblables à des arbres à l’intérieur de la Sagrada Familia ou même au dallage barcelonais marqué de l’hélice des escargots. L’art nouveau de Gaudí passionne les écoles d’art et d’architecture, mais aussi la mode (voir la collection automne/hiver 2015-2016 de Max Azria) et fera d’ailleurs l’objet d’une exposition évènement au Musée d’Orsay en 2022.

L’influence des réseaux sociaux
Si depuis l’antiquité, l’équilibre des formes a guidé nombre de créations à l’origine de ce que l’on appelle les « beaux-arts », les médias du XXIᵉ siècle ne sont pas en reste et ont su intégrer ces codes. Du nombre d’or à la règle des tiers.) en photographie comme au cinéma il n’y a qu’un pas. Les instagrammeurs ont bien compris l’intérêt d’une photographie esthétiquement équilibrée et soignée grâce au nombre d’or et le feed Instagram (le portfolio personnel de chaque utilisateur) n’est-il pas une juxtaposition de trois colonnes permettant à tout un chacun des associations d’images et d’idées poétiques sur la toile ?
Héritiers d’une longue histoire des images, nous avons tendance à les reproduire instinctivement ou à aimer les proportions les plus familières. Le compte @instarepeat le prouve : la prégnance de certains clichés en a fait des standards non seulement parce qu’ils invitent au voyage, à la poésie, mais aussi parce qu’ils nous renvoient à une expérience esthétique « confortable » pour notre œil habitué à certaines proportions. Les utilisateurs des réseaux se mettent en scène avec un même objectif dans des photographies qui dictent et reflètent des critères de beauté certes, mais à travers la reproduction plus ou moins consciente de lignes de fuite ou de proportions aptes à retenir l’attention, ils sont eux aussi sous l’influence du nombre d’or.

L’équilibre du corps et des compositions artistiques est le reflet de valeurs sociales en constante évolution, au même titre que la perception du beau d’une époque à l’autre. Par abus de langage, parler du nombre d’or ou revendiquer son usage revient simplement à parler du beau ou du sens de l’harmonie. Nombre de mathématiciens démentent l’intérêt de ce nombre et soulignent que certaines formes ou objets jugés assez universellement comme harmonieux ne relèvent pas du tout de cette proportion. Dans l’histoire récente des sciences dures, le nombre d’or semble susciter peu d’intérêt.
A contrario, il continue de fasciner et d’inspirer les artistes, à la manière d’un mythe ou d’une notion mystique. Son nom lui-même a quelque chose de fascinant, comme une clé magique et mystérieuse qui permettrait de créer du beau. Le nombre d’or fascine parce qu’il est une sorte de nœud où s’entremêlent un concept mathématique et des transpositions esthétiques dans des domaines très variés, attestant de son aura mythique qui ne risque pas de perdre du terrain à une époque de plus en plus préoccupée par l’image et l’esthétique.
L’autrice de cet article le dédie aux étudiants de Master 2, Management International Trilingue, marchés hispanophones (2021-2022) de l’Université Paris-Est Créteil qui ont enrichi de leur réflexion le cours « Art, publicité et marketing : étude de cas du marché hispanophone ».
Sabrina Grillo, Maîtresse de conférences en civilisation de l’Espagne contemporaine, Université Paris-Est Créteil Val de Marne (UPEC)
Este artículo fue publicado originalmente en The Conversation. Lea el original.
Article original du site Live Sensei

